Distributions-
o Binomial distribution-
Probabilities of the number of successes over a given number of trials-
o Normal Distribution- X is normal random variable (mean = µ, variance = σ2). PDF for the
normal distribution.
o
Poisson
Distribution- Average number of successes = ʎ, Poisson probability of k
successes
o Geometric distribution- Number
of trials X it takes to get the first success has a geometric distribution.
o Chi-Square Distribution- used for goodness of fit
and in CI estimation
for a PSD (s) from SSD (s).
o Cauchy distribution- µ and s2 are
undefined. Mode and median are defined and equal to x0.
Location
parameter can be mean, median or mode and Scale parameter can be variance, s etc.
o Weibull Distribution- Lognormal
distribution, change in parameter changes shape and in turn skewness.
o Joint Distribution Function-
o Marginal distributions- Distribution
of each variable separately. If independent, than pxy(s,t) = px(s)
* py(t).
o Conditional Distribution and
Expectation-
o
Inequalities-
a) Jensen's Inequality- -
b)
Markov’s
inequality- gives an upper
bound of P such that +ve
random variables ³ +ve constant.
c)
Tchebychev’s
inequality- gives an upper bound of P such that -ve random variables ³ -ve constant.












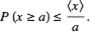

No comments:
Post a Comment